Basics of separation logic
Separation logic is an extension of Hoare's logic oriented to reasoning about mutable data structures (or, programs with dynamically allocated pointers). It enables more compact proofs and specs of imperative programs than before because of its support for local reasoning, where specifications and proofs concentrate on the portion of memory used by a program component, and not the entire global state of the system.
Separating conjunction & the frame rule
Separation logic assertions describe heaps. Besides the normal logical connectives (conjunction, disjunction, implication, etc), SL introduces the separating conjunction ( ) of two assertions. A heap satisfies the separating conjunction of two assertions if it can be divided into two disjoint parts satisfying the two assertions. Formally,
) of two assertions. A heap satisfies the separating conjunction of two assertions if it can be divided into two disjoint parts satisfying the two assertions. Formally, 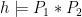 if and only if there exist (disjoint)
if and only if there exist (disjoint) 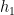 and
and 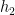 such that
such that 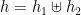 and
and 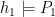 and
and 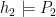 .
.
The frame rule is the crux of local reasoning:
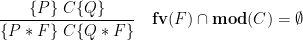
It says that a program that runs correctly with a heap satisfying the precondition, 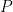 , also runs correctly with a bigger initial heap,
, also runs correctly with a bigger initial heap, 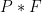 . Further, the program is guaranteed not to touch the additional portion of heap, and so
. Further, the program is guaranteed not to touch the additional portion of heap, and so 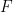 remains true in the postcondition. Therefore, programs specifications need only describe the footprint of the program (i.e., the part of the heap it accesses). Using the frame rule, these specifications can be applied in any larger context.
remains true in the postcondition. Therefore, programs specifications need only describe the footprint of the program (i.e., the part of the heap it accesses). Using the frame rule, these specifications can be applied in any larger context.
Introductory material
Separation Logic: A Logic for Shared Mutable Data Structures. JC Reynolds. In LICS 2002. This is the best introduction to separation logic.
Extensions & tool support
There are numerous extensions of separation logic for better handling:
- Abstraction (hypothetical frame rule, abstract predicates, context logic)
Concurrency (CSL, locks-in-the-heap, RGSep/SAGL/LRG, deny-guarantee)
- Assembly code
- Higher-order functions
There are also many SL-based tools such as entailment provers and static analyzers. For more information, see ToolSupport.
Further reading
TODO
