Mechanized Program Verification and Analysis with Separation Logic

Several tools have been developed for mechanizing separation logic proofs, ranging from interactive tools to fully automatic tools. This page focuses on more automatic approaches. For the other end of the spectrum, go to:

Separation logic in proofs assistants

Semi-automatic verification tools

Tools in this category typically require user-provided pre/post specifications for each function, loop invariants, and resource invariants for concurrent programs. First steps in this direction were taken in the Smallfoot project (2002-2005).

Symbolic Execution with Separation Logic. J Berdine, C Calcagno and PW O'Hearn. In APLAS 2005, LNCS 3780.
Smallfoot: Modular Automatic Assertion Checking with Separation Logic. J Berdine, C Calcagno and PW O'Hearn. In FMCO 2006, LNCS 4111.

Smallfoot did verification by symbolic execution interspersed with entailment checking, rather than the "vcgen" method. Formulae were updated in-place, which obviated the need for complex alias checking. Smallfoot did automatic proofs of lightweight safety properties of programs, mimicking the proofs done by hand in most of the early separation logic papers, up to and including Concurrent Separation Logic.

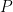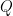Symbolic execution is based on solving the frame inference problem: Given and find the strongest assertion 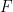such that 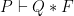$P \vdash Q * F$ if one exists, or fail otherwise. For efficiency and/or decidability reasons, the provers often return slightly weaker assertions and may even fail to prove valid entailments.

Other tools

Heap-Hop (Paris): Smallfoot extension for message-passing programs.
Hip (Singapore)
jStar (London/Cambridge): SL-based verifier for Java programs.
SmallfootRG (Cambridge): Smallfoot extension for fine-grained concurrent algorithms.
Verifast (Leuven): verifier for Java and C.

Automatic verification tools

Tools in this category do not require any annotations except perhaps for the specification of the program to be verified. The tools are responsible for finding suitable loop invariants and, in case of concurrent programs, also resource invariants or rely-guarantee conditions.

CAVE (Cambridge/Kaiserslautern): verifies linearizability of fine-grained concurrent algorithms (using a variety of techniques in addition to SL).
Space Invader (London)
SLAyer (Cambridge): MS Windows device drivers.
THOR (Pittsburgh): generates integer programs abstracting the SL proof.
Xisa (Colorado/Paris): supports user-defined inductive data structures.

These tools infer invariants via a fixed-point calculation in a suitable abstract domain, in the usual manner of abstract interpretation. Some results in this area are:

A local shape analysis based on separation logic. D Distefano, P O'Hearn and H Yang. In TACAS 2006, LNCS 3920, pp287-302.
This paper introduces the domain of singly linked non-empty list segments.
Scalable Shape Analysis for Systems Code. H Yang, O Lee, J Berdine, C Calcagno, B Cook, D Distefano and P O'Hearn. CAV 2008.
This paper shows a carefully designed join operation for scaling shape analysis to entire Microsoft and Linux device drivers of up to 10K LOC.
Compositional Shape Analysis by means of Bi-Abduction. C Calcagno, D Distefano, PW O'Hearn and H Yang. POPL 2009.
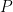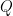This paper extends the frame inference question to a bi-abductive inference question: Given and find 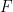(the frame) and 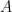(the anti-frame) such that 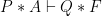$P * A \vdash Q * F$ . The paper describes an ordering on the solutions to this problem and an incomplete, but useful, solver that was applied to infer pre/post procedure specs without knowing the calling context at a much larger scale (> 1M LOC).