Concurrency & Local Reasoning
The concepts of ownership and separation from separation logic naturally apply to concurrent programs. This is best illustrated by the disjoint parallel composition rule:
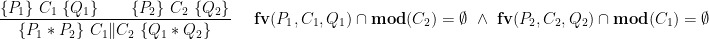
The rule says that if two threads execute on disjoint portions of the heap, they can safely be run in parallel. The side-condition states that each thread does not modify the variables mentioned by the other thread, thereby ensuring that there are no race conditions on program variables. This rule allows us to reason about simple parallel programs such as parallel merge sort without requiring rely-guarantee conditions; each thread simply minds its own business.
To handle concurrent programs where threads do interact with each other, a number of extensions have been proposed:
CSL (Concurrent Separation Logic)
CSL (O'Hearn 2007) adapted resource invariants to separation logic and introduced the notion of 'ownership transfer,' whereby the right to access a portion of the heap can be transferred between processes via a shared resource invariant. This enables modular reasoning in the presence of semaphores (e.g., split binary semaphores without maintaining a global invariant).
CSL specifications consist of a precondition, a postcondition, and a resource environment Γ mapping resource names to resource invariants (which are separation logic assertions). The resource environment, Γ, is simply threaded through all the standard SL rules, and gets used in the following two rules:
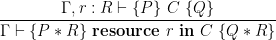
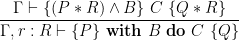
The first rule declares a new resource,  , with invariant
, with invariant  . Naturally, the invariant must hold separately of the precondition and is guaranteed to remain true in the postcondition. The second rule allows us to use the state protected by the resource,
. Naturally, the invariant must hold separately of the precondition and is guaranteed to remain true in the postcondition. The second rule allows us to use the state protected by the resource,  . To do so, we must execute a conditional critical region (CCR), within which we can assume that its resource invariant holds initially and have to reestablish it when exiting the CCR.
. To do so, we must execute a conditional critical region (CCR), within which we can assume that its resource invariant holds initially and have to reestablish it when exiting the CCR.
Ownership
In CSL terminology, a thread with a precondition 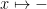 owns the memory cell pointed to by x. Ownership is a promise that the program will not access any portion of the heap outside its ownership domain and an assumption that the program is the sole owner of the portion of the heap described by its precondition. This concept that appears only in the correctness proof of a program and is enforced by the CSL proof rules. In O'Hearn's terms, Ownership is in the eyer of the beholder.
owns the memory cell pointed to by x. Ownership is a promise that the program will not access any portion of the heap outside its ownership domain and an assumption that the program is the sole owner of the portion of the heap described by its precondition. This concept that appears only in the correctness proof of a program and is enforced by the CSL proof rules. In O'Hearn's terms, Ownership is in the eyer of the beholder.
Permissions (due to Boyland) are an extension of notion of ownership with the concept of a partial owner. In CSL with permissions, full ownership of a memory cell can be decomposed (with the separating conjunction) into two half permissions, each allowing its beholder to read from the memory cell, but not to update it. A half permission can further be decomposed in two quarter permissions, each of which still allows one to read from the memory cell, and so on. Finally, two half permissions can be recombined (with the separating conjunction) into a full permission, allowing both read and write access to the memory cell.
Deny-guarantee further refines the notion of ownership and permissions so that the ability to do any particular change (such as change the value of x from 0 to 1) is subject to ownership, full or partial. Moreover, in deny-guarantee there are two kinds of partial ownership, one which allows everybody to do the change, and one which forbids everybody to do the change.
Ownership transfer
The CCR proof rule allows the ownership of a memory cell to be transferred in and out of the resource invariant, 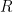 . For example, let
. For example, let 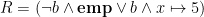 . Then a thread can execute the CCR
. Then a thread can execute the CCR 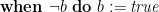 to add a memory cell to the critical region or
to add a memory cell to the critical region or 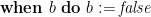 to remove it from the region.
to remove it from the region.
Further examples can be found in O'Hearn (2007).
Soundness
Proving the soundness of CSL has historically been quite tricky. O'Hearn writes: "... At that time [Jan. 2002] I had no model and was scared about soundness. Then John Reynolds showed surprising subtleties regarding soundness, and we were facing an extremely difficult problem in the semantics of concurrency. We needed expert help, and it arrived in Steve Brookes who rode in and saved the day (and the whole approach)." The subtleties that O'Hearn refers to are the interaction of the conjunction, frame, and CCR rules, which can lead to unsoundness of the logic (cf. the Reynold's counterexample in O'Hearn (2007)). The usual remedy is to require resource invariants to be precise assertions. An alternative is to drop the conjunction rule.
The first proof of soundness was due to Brookes (2007) over a denotational trace semantics for programs and using an intermediated instrumented semantics for carrying out the proof. Later proofs have been done by Hayman (2006), Gotsman (2009), Hobor (2008), and others. Recently, Vafeiadis has proposed a simpler operational proof with dispenses the need of an intermediate semantics.
A semantics for concurrent separation logic. SD Brookes, Theoretical Computer Science 375(1-3) (Reynolds Festschrift), pp227-270, May 2007.
Independence and concurrent separation logic. J Hayman and G Winskel. LICS 2006
Moderate Extensions
- Permissions
Checking Interference with Fractional Permissions. J Boyland. SAS 2003.
Permission Accounting in Separation Logic. R Bornat, C Calcagno, PW O'Hearn, M Parkinson. POPL 2004.
Storable locks; a.k.a. locks in the heap
Local reasoning for storable locks and threads. A Gotsman, J Berdine, B Cook, N Rinetzky, M Sagiv. APLAS 2007
Oracle semantics for concurrent separation logic. A Hobor, AW Appel, F Zappa Nardelli. ESOP 2008.
- Reentrant locks
- Other synchronization constructs
Proving copyless message passing. J Villard, E Lozes, C Calcagno. APLAS 2009.
Barriers in concurrent separation logic. A Hobor, C Gherghina. ESOP 2011.
Criticism
Although the notion of ownership transfer introduced by O'Hearn has been very useful in reasoning about concurrent programs, CSL itself has been criticized for two shortcomings:
Because resource invariants are assertions of a single state, CSL proofs of intricate concurrent algorithms often require many auxiliary variables. This leads to ugly, un-modular proofs, a large part of which is spent working around the limitations of the logic. A good example of such an ugly proof by the verification of a non-blocking stack by Parkinson, Bornat, and O'Hearn (2007). Vafeiadis in his PhD thesis argued that predicates describing transitions (two-states) were necessary and that RGSep is a better –albeit not perfect– logic for reasoning about intricate concurrent algorithms. Jacobs and Piessens (2011) showed that modularity in CSL can be reinstated by writing specifications in a higher-order style up to auxiliary variable insertion. Nevertheless, CSL proofs of intricate concurrent algorithms remain largely impractical.
The sheer number of CSL extensions for each different concurrent primitive suggests that CSL itself the wrong formalism, because ideally the specifications for these constructs should be derivable within the same logic. Parkinson (2010) suggested that deny-guarantee with (concurrent) abstract predicates might be the 'correct' formalism.
Main papers
Resources, concurrency and local reasoning. PW O'Hearn, Theoretical Computer Science 375(1-3) (Reynolds Festschrift), pp271-307, May 2007.
A semantics for concurrent separation logic. SD Brookes, Theoretical Computer Science 375(1-3) (Reynolds Festschrift), pp227-270, May 2007.
